The purpose of this project is to come up with a very basic an rough mathematical model of the Islamic Banking system and the Traditional banking system. The idea is to compare and see the differences, similarities and how they may affect an entity involved in these systems.
Full Disclosure: The model is very basic an is designed in such a way that it could be understood by someone with a bit of basic calculus knowledge and experience. The models are based on the simple concepts of profit and loss. Nothing major. I am not a scholar of Islamic Finance hence my knowledge in this is very shallow. I have just used common assumptions and variables when modeling these. Feel free to correct me where I have gone wrong (check my contact page if need be).
Some concepts of the two systems
For our purposes, we will only consider the scenario of a bank giving out a “loan” to a business and how the business and the bank benefits from each other.
In Islamic Banking (Finance), the concept of interest is non-existent. It operates on sharing profits and losses. That is, if a client C wanted to start a business but does not have enough capital, then they may request for some amount of initial capital C0 from an Islamic Bank I. The policy for I is that instead of charging interest on C0 on C, I would share some percentage of the profit/loss gained by C over a period of time. This is to say that the amount C0 will be repaid to I as well some amount of profit gained by C for a limited period of time. This amount may be a percentage p.
In Traditional Banking, the bank T gives out a loan to C. And as a method of repayment, T charges an interest (mostly compound interest) with rate i on the initial capital C0. The client C has to repay the total amount with interest regardless of whether C makes any profit or not.
Variables
- The earning of Islamic Bank, I
- The earning of Traditional Bank, T
- The earning of client, C
- Initial capital given by I and T to C, C0
- Percentage profit/loss shared by I and C, p
- Interest rate of T, i
- A time period, t
Assumptions
- The earning C is ideal and grows exponentially over time (assuming the business grows and opens new branches).
- To have a “fair” earning rate for both I and T, the values of p and i are equal, i.e. p=i.
The Models
Model of C’s growth
Using the above assumptions, it can be concluded that C is a function of t and can be modelled as
\[C(t) = C_{0}\text{exp}(\alpha t)\]
where, \(\alpha\) is a constant.
The profit made by the client at any given time \(t\) can be derived to be the following:
\[C'(t) = C_{0}\alpha\text{exp}(\alpha t)\]
And the following is my reasoning.
The total revenue at any given time \(t\) is \(C(t)\). Hence the revenue in the next time period is \(C(t + \Delta t)\). Then it follows that the profit gained in time \(\Delta t\) is \(C(t + \Delta t)-C(t)\). Hence the rate of profit gained is the profit divied by \(\Delta t\). Therefore if we take the limit as \(\Delta t \to \infty\) we obtain the following expression:
\[\lim_{\Delta t \to \infty} = \frac{C(t + \Delta t) - C(t)}{\Delta t} = C'(t)\]
Model of I’s earning
Based on the concept above, it can be concluded that \(I\) is a function of \(t\) and depends on the function \(C'(t)\) and the constant \(p\). Hence our model becomes:
\[I(t) = pC'(t)\]
\[I(t) = pC_{0}\alpha\text{exp}(\alpha t)\]
And the rate at which this profit increases is the function \(I'(t) = pC_{0}\alpha^{2}\text{exp}(\alpha t)\)
From this we can deduce the net profit of the client can be given by:
\[C^\ast = C(t) - I(t)\]
\[C^\ast = (1-p) C_{0}\alpha\text{exp}(\alpha t)\]
Model of T’s earning
Traditional banks use mostly compound interest when they give out loans to businesses. Hence the following can be deduced:
\[T(t) = C_{0}{(1+i)}^{t} - C_{0}\]
Similarly the rate of increase in T’s profit is simply the function \(T'(t) = \ln(1+i)C_{0}{(1+i)}^{t}\)
From the previous expressions, we can derive that C’s net profit my be given by the expression:
\[C^{\ast\ast} = C_{0}\alpha\text{exp}(\alpha t) - C_{0}{(1+i)}^{t} + C_{0}\]
Parameter values
- \(C_{0} = 100,000\) for the initial capital
- \(p = i = 0.10\) as the profit and interest rates
- \(\alpha = 0.9\) for best case
- \(\alpha = 0.2\) for intermediate case
- \(\alpha = 0.05\) for worst case
- \(t = 10\) with values from \([0,10]\) with 1 step increment
Results
The code for the model can be found here. There are three Jupyter Notebooks (Python Codes) for the best, intermediate and worst cases.
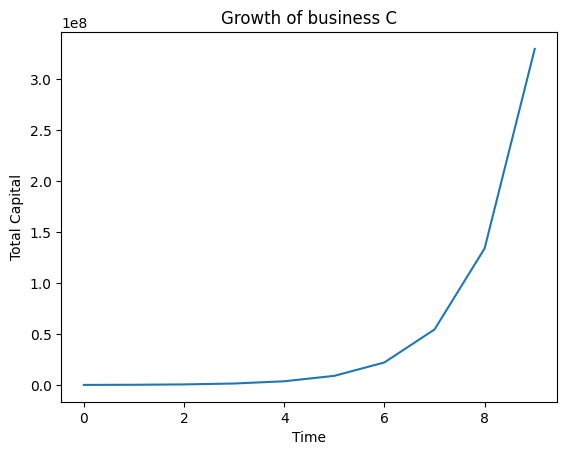
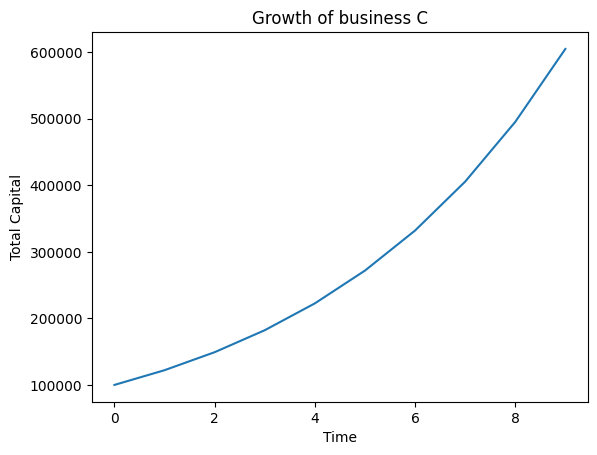
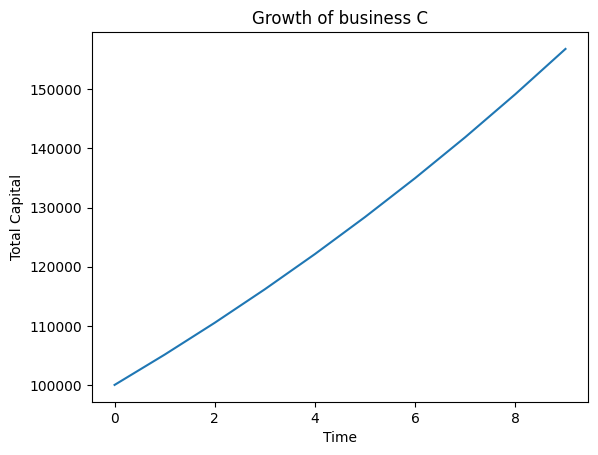
Growth of C
The following graphs show the best, intermediate and worst case for the growth of C (in that order)
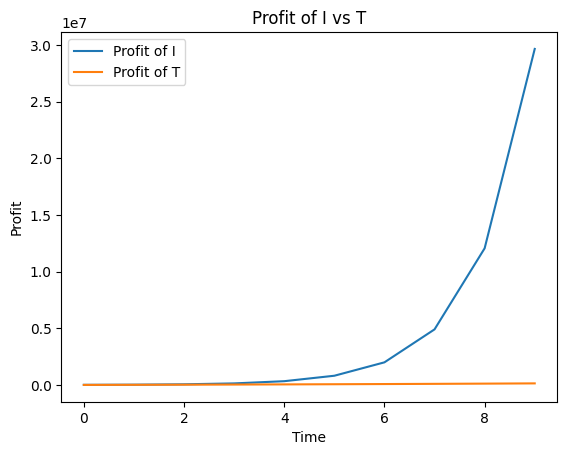
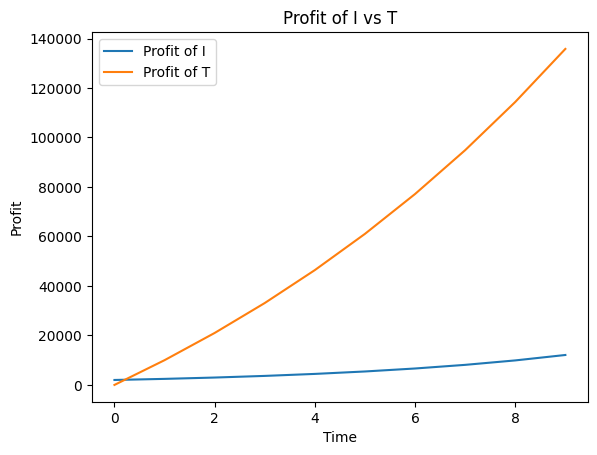
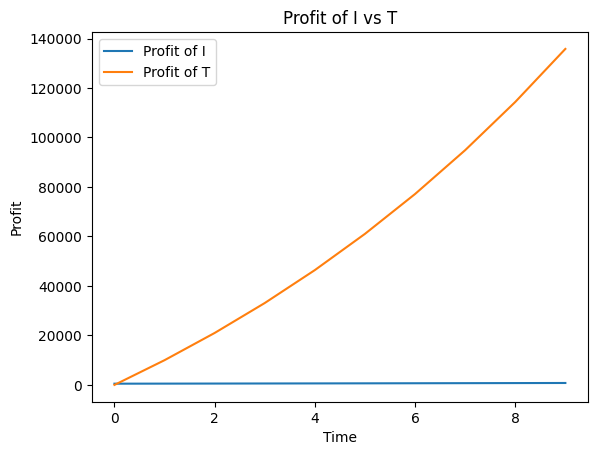
Profit of I vs T
These graphs compare the profits earned by I and T using the best, intermediate and worst case growth of C (in that order)
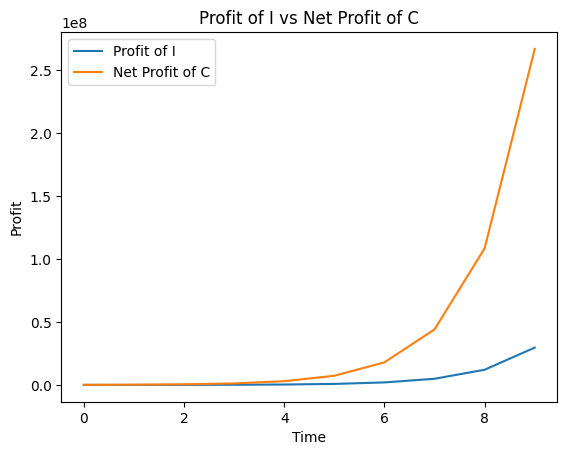
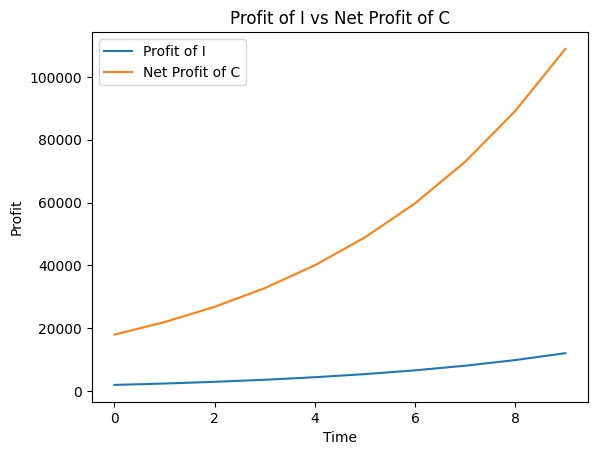
Profit of I and C
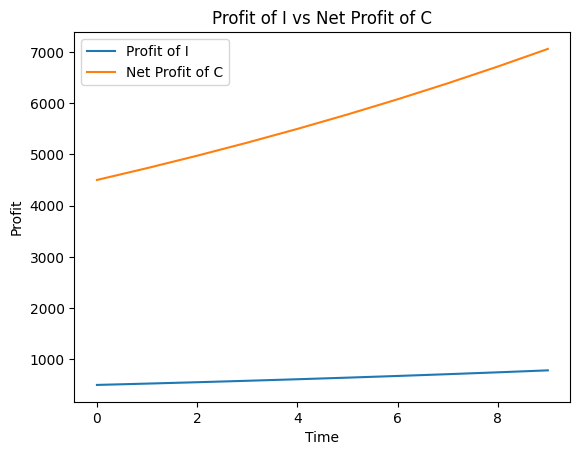
The following graphs compare how both I and C gain profits using the same order of cases as above
Profit of T and C
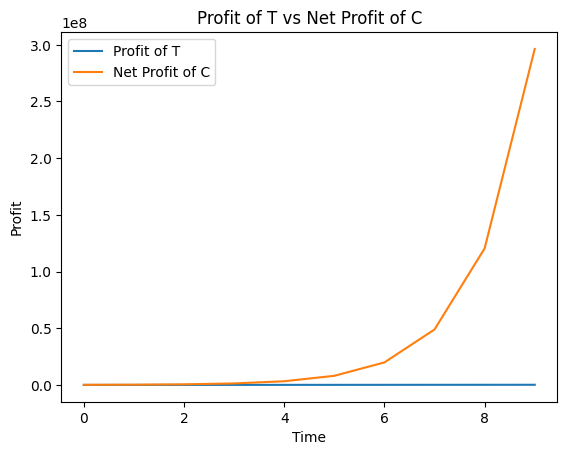
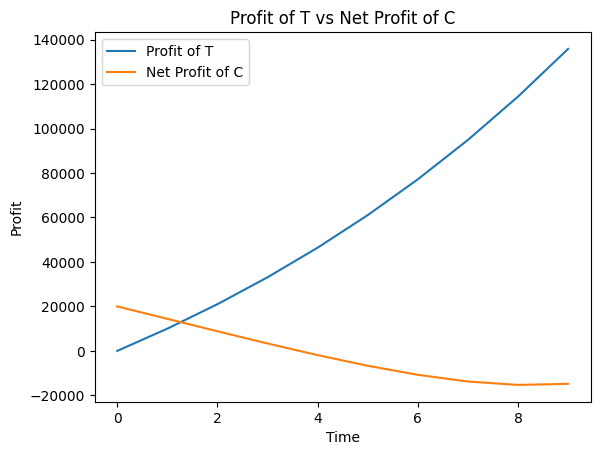
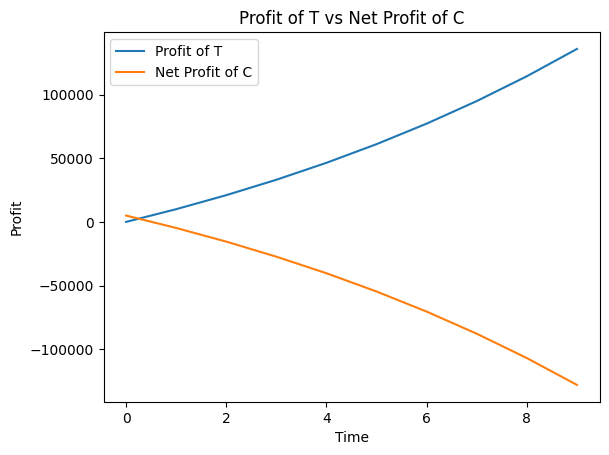
The following graphs compare how T’s and C’s profits evolve over time using the same order of cases as above
Discussion
In this best case scenario, where C’s growth is very good, I and C manage to make profits. However, T makes less profit over the years as compared to I. This might be beneficial to the community as I will now be able to help out more businesses with more investments in each business.
In this intermediary scenario, where C’s growth is quite good, I and C still manage to make profits. However, T manages to make more profit over the years than I. But the net profit of C declines over the years where at year ~3.5, C starts making losses.
In this worst case scenario, where C’s growth is okay (almost linear), I and C still manage to make profits although the rate is slow. However, T makes more profit than I. This may be good for T but C loses out as its business model cannot cope with the interest rates over the years. Hence C makes losses from the very beginning and the business shuts down.
Conclusion
Using a bit of “basic” mathematics, we are able to witness that the Islamic Banking system is better than the traditional banking system. This has been just a rough model. This is part 1. In part 2, I will try and model how these systems may affect the economic systems and balance of a country. Keep in mind that one can make the model as complex as they would like. This is just the tip of the iceberg and a proof of concept. Please feel free to correct me where I might have made mistakes and suggest on how this model can be improved further.